ATD: Surveillance Evasion and Threat Avoidance

---

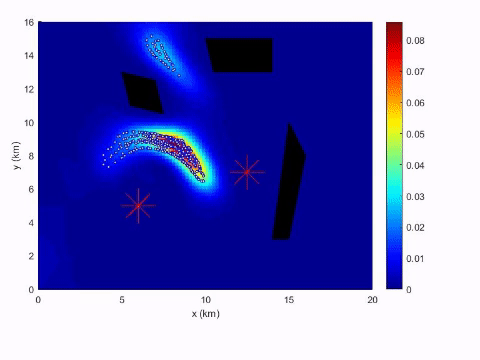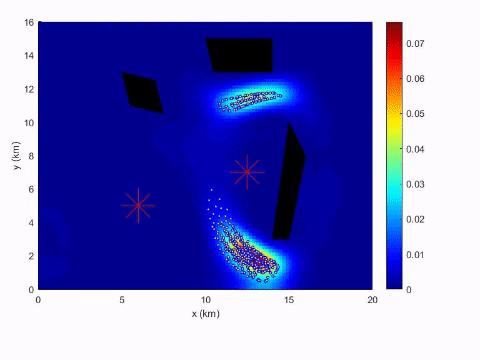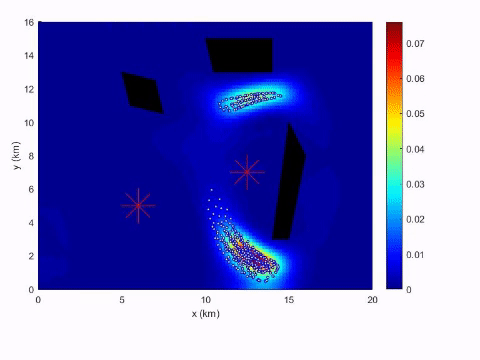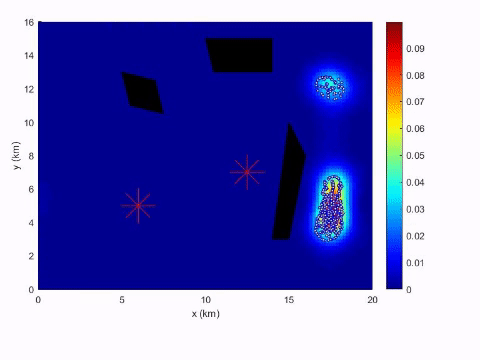
September 1, 2017 – October 31, 2020                                                                                 $400,000

---

---

Project Description

This project seeks to use tools from optimal control theory to design efficient methods for two such models:

• Civilians in dangerous environments (e.g., war zones) will primarily plan their paths to minimize the threat exposure.
• Adversaries aware of the existing monitoring measures will plan their paths to evade the observation.

Research Goals

• The forward problem: How will people plan their paths given the full information about the environment?
• The inverse problem: Given sparse information about their route choices or travel times, how can we infer beliefs about the environment?
• The adversarial problem: What should people do to optimize their cost under uncertainty about the location of threats or observers? How might the environment change in response to their choice?

Peer-Reviewed Publications

1. J. Morelli, P. Zhu, B. Doerr, R. Linares, S. Ferrari “Integrated Gas Distribution Mapping and Path Planning for Very Large-Scale Robotic (VLSR) Systems,” Sensors, submitted.
2. J. Morelli, P. Zhu, B. Doerr, R. Linares, S. Ferrari “Integrated Mapping and Path Planning for Very Large-Scale Robotic (VLSR) Systems,” ICRA, submitted.
3. B. Doerr, R. Linares, P. Zhu, S. Ferrari “Random Finite Set Theory and Optimal Control for Large Spacecraft Systems”, AIAA.

Presentations

1. “Time-dependent Surveillance-evasion Games,” Research Experience for Undergraduates (REU), Cornell, July 25, 2018. [PDF]